视频编解码
A generic codec
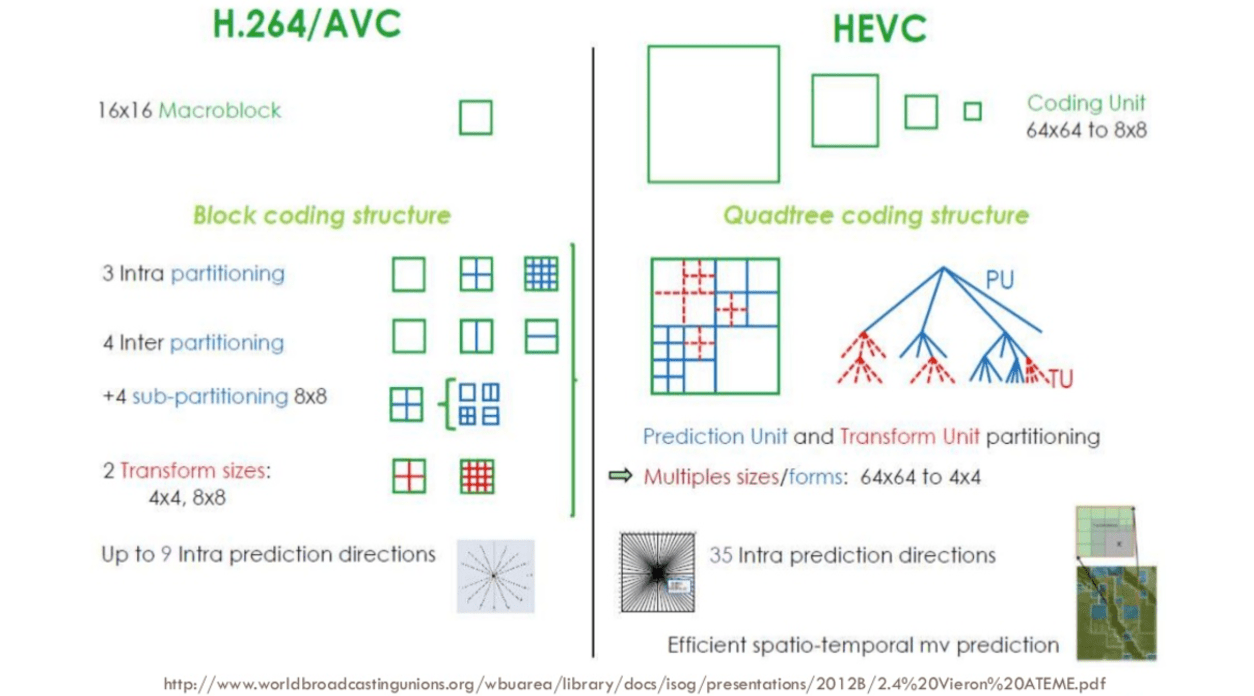
1st step - picture partitioning
The first step is to divide the frame into several partitions, sub-partitions and beyond.
Work the predictions more precisely
- smaller partitions for the small moving parts
- bigger partitions to a static background.
Usually, the CODECs organize these partitions into:
- slices (or tiles)
- macro (or coding tree units)
- sub-partitions.
- macro (or coding tree units)
frames are typed:
- I-Slice
- B-Slice
- I-Macroblock
- and etc.
2nd step - predictions
Once we have the partitions, we can make predictions over them. For the inter prediction, we need to send the motion vectors and the residual and the intra prediction we’ll send the prediction direction and the residual as well.
- Temporal redundancy (inter prediction)
- Spatial redundancy (intra prediction)
3rd step - transform
After we get the residual block (predicted partition - real partition), we can transform it in a way that lets us know which pixels we can discard while keeping the overall quality. There are some transformations for this exact behavior.
Although there are other transformations, we’ll look more closely at the discrete cosine transform (DCT). The DCT main features are:
- converts blocks of pixels into same-sized blocks of frequency coefficients.
- compacts energy, making it easy to eliminate spatial redundancy.
- is reversible, a.k.a. you can reverse to pixels.
We might notice that the first coefficient is very different from all the others. This first coefficient is known as the DC coefficient which represents all the samples in the input array, something similar to an average.
This block of coefficients has an interesting property which is that it separates the high-frequency components from the low frequency.
In an image, most of the energy will be concentrated in the lower frequencies.
Thus,if we transform an image into its frequency components and throw away the higher frequency coefficients, we can reduce the amount of data needed to describe the image without sacrificing too much image quality.
4th step - quantization
When we throw away some of the coefficients, in the last step (transform), we kinda did some form of quantization. This step is where we chose to lose information (the lossy part) or in simple terms, we’ll quantize coefficients to achieve compression.
How can we quantize a block of coefficients? One simple method would be a uniform quantization, where we take a block, divide it by a single value (10) and round this value.
How can we reverse (re-quantize) this block of coefficients? We can do that by multiplying the same value (10) we divide it first.
This approach isn’t the best because it doesn’t take into account the importance of each coefficient, we could use a matrix of quantizers instead of a single value, this matrix can exploit the property of the DCT, quantizing most the bottom right and less the upper left, the JPEG uses a similar approach, you can check source code to see this matrix.
5th step - entropy coding
After we quantized the data (image blocks/slices/frames) we still can compress it in a lossless way. There are many ways (algorithms) to compress data. We’re going to briefly experience some of them, for a deeper understanding you can read the amazing book Understanding Compression: Data Compression for Modern Developers.
- VLC coding:
Let’s suppose we have a stream of the symbols: a, e, r and t and their probability (from 0 to 1) is represented by this table.
We can assign unique binary codes (preferable small) to the most probable and bigger codes to the least probable ones.
Let’s compress the stream eat, assuming we would spend 8 bits for each symbol, we would spend 24 bits without any compression. But in case we replace each symbol for its code we can save space.
The first step is to encode the symbol e which is 10 and the second symbol is a which is added (not in a mathematical way) [10][0] and finally the third symbol t which makes our final compressed bitstream to be [10][0][1110] or 1001110 which only requires 7 bits (3.4 times less space than the original).
Notice that each code must be a unique prefixed code Huffman can help you to find these numbers. Though it has some issues there are video codecs that still offers this method and it’s the algorithm for many applications which requires compression.
Both encoder and decoder must know the symbol table with its code, therefore, you need to send the table too.
- Arithmetic coding:
Let’s suppose we have a stream of the symbols: a, e, r, s and t and their probability is represented by this table.
With this table in mind, we can build ranges containing all the possible symbols sorted by the most frequents.
Now let’s encode the stream eat, we pick the first symbol e which is located within the subrange 0.3 to 0.6 (but not included) and we take this subrange and split it again using the same proportions used before but within this new range.
Let’s continue to encode our stream eat, now we take the second symbol a which is within the new subrange 0.3 to 0.39 and then we take our last symbol t and we do the same process again and we get the last subrange 0.354 to 0.372.
We just need to pick a number within the last subrange 0.354 to 0.372, let’s choose 0.36 but we could choose any number within this subrange. With only this number we’ll be able to recover our original stream eat. If you think about it, it’s like if we were drawing a line within ranges of ranges to encode our stream.
The reverse process (A.K.A. decoding) is equally easy, with our number 0.36 and our original range we can run the same process but now using this number to reveal the stream encoded behind this number.
With the first range, we notice that our number fits at the slice, therefore, it’s our first symbol, now we split this subrange again, doing the same process as before, and we’ll notice that 0.36 fits the symbol a and after we repeat the process we came to the last symbol t (forming our original encoded stream eat).
Both encoder and decoder must know the symbol probability table, therefore you need to send the table.
6th step - bitstream format
After we did all these steps we need to pack the compressed frames and context to these steps. We need to explicitly inform to the decoder about the decisions taken by the encoder, such as bit depth, color space, resolution, predictions info (motion vectors, intra prediction direction), profile, level, frame rate, frame type, frame number and much more.